Rocket science is no rocket science. Nothing is ever rocket science. And nobody is ever just “bad at math.”
“Wow, another engineering student trying to convince me that math is easy just because he’s good at it. Amazing!”
If I still had it, I’d proudly attach to this post each of my five high school transcripts: all average/high marks, until the “Math” and “Physics” lines. For those, you could see my shiny 6/10 (veeeery kindly rounded up out of a 5.4/10).
“But he’s an engineering student now, he likes stuff like programming, data science, AI; it must have been because of a scrappy math and physics teacher!”
Oh boy, you have no idea how much I wish it were like that. During university, my struggle amplified: calculations became extremely more complex, increasingly abstract concepts started to pop up, and my inner mathematician began drinking heavily, losing the whole point of its life.
Each time a new concept was introduced, I was nearly always missing the point of the previous two (at least) topics, which, as you can guess, was very upsetting and frustrating. Not only did I feel frustrated, but I began questioning the whole point of studying differential equations or plotting a Nyquist plot.
If the point of what you’re spending your weeks on starts faltering, and your thoughts start sounding like “Who cares about what an integral does? An engineer never computes an integral!” I’m afraid that this post suits you, especially if you’re a freshman.
I wrote this post to sum up what I wish I knew at the beginning of my university journey so that you don’t have to struggle as much as I did!
Let’s start by listing the problems:
- Nobody has ever even tried to show me the practical side of what we were doing. All theory, no real world.
- When a step (even a small one) was skipped, I would lose a piece and panic.
- Study material was very, very incomplete (and a lot of steps were skipped there!).
- It’s (almost) all about memory.
Does at least one of those ring a bell? I really hope it doesn’t, but in case it does, I’d like to explain to you, dear reader, how I set up my study and lesson routine, (almost) managing to overcome the aforementioned problems.
What happens in Real Life?

“Do you know what this is?“
“No.” ”What kind of an engineer are you? Shame! Shame on y-
“Oh, I know that! That’s a Capacitor!”
Don’t you see something terribly wrong with this?
Electronics is such a fascinating field of physics, and we can easily observe that in real life! Despite that, within a whole semester, I (along with thousands of students) have never been exposed to the material existence of a single diode.
Why does that happen? Why on earth should we prefer rooting for a 100% theoretical university that quickly covers 100 topics instead of a hybrid one that makes students touch what their differential equations mean, investing time in deeply understanding 60 topics? Why are we choosing quantity over quality?
I know that theoretical-only lectures are an all-Italian tradition (dear international students, I’d love to hear your thoughts on this, drop a comment, please!), so this part might leave international readers stunned (hopefully!). But I believe this is one of the worst features of the Italian university system that immediately needs to be fixed.
I believe that building a strong association between theoretical and practical knowledge has been the #1 contributor to the worldwide interest in software engineering. I struggle to think about another subject that has such deep mathematical implications while getting along with extremely fun exercises.
How am I supposed to feel some connection with mechanics just by studying Tresca’s theorem? Every subject should include a lab experience at a certain point, or a final project, even a small one, even a CAD simulation, even one hour/month of supervised practice time—just enough to make the “naturally uninterested” student feel like things are actually cooler than he thinks.
Let’s go Step by Step
I recently completed the Supervised Machine Learning course by DeepLearning.AI. There would be dozens of reasons why I’d recommend this course, but two of those particularly fit this paragraph:
- Constant recalls to important concepts.
- Steps were never skipped.
So easy, but so powerful: not even once did I need to pause the video and CTRL-F around my notes, because everything was already there; even old concepts were quickly re-defined if needed! Awesome! Clear! Moreover, during the (pretty straightforward) math steps, none was skipped, allowing everybody to go through the whole process without asking ChatGPT, “How did we get to this step?”
When I think about the days in which I attended Calculus 1 and Calculus 2 classes, I can still feel the confusion due to a single (and often quite easy) step loss. Those steps could have been anything: a normal differentiation, replacing some “cos(x)^2+sin(x)^2” with a 1 without stating it—anything!
Study material:
Let me introduce you to the wonderful material that our Calculus 2 professor handed us, applying some cutting-edge worldwide teaching techniques:
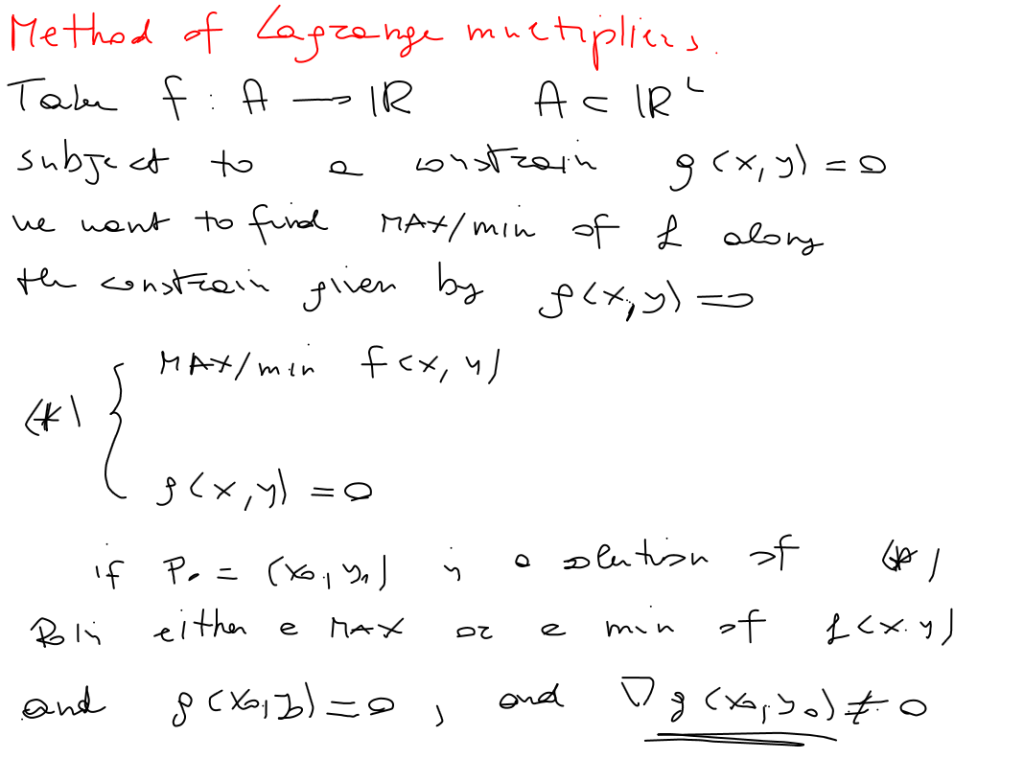
Clear, isn’t it? Questions?
No graphs, no book, no nothing. Just a scrappy drawing tablet and a wonderful white background, not even a squared sheet one.
It goes without saying that I desperately needed some more material to study, so I began googling, but it would have taken me more than that, as I soon discovered.
A matter of Memory?
Old school teaching comes with an inborn bug: you can get a high mark by memorizing sentences without really getting what’s behind the words.
I lost count of how many times my brain went:
“Why the hell are we applying this rule? What does it mean?”
“Shut up”, me, “teacher didn’t say it, thus it’s nothing we care, plus he’ll never ask us that!”
This little loop of reasoning, I believe, is the most toxic way to approach learning: as a matter of fact you won’t learn pretty much anything, since you’ll only focus on getting a grade and heading to the next test.
I believe what I’m about to say is pretty common within your experience, dear reader, especially if you come from the Italian way of teaching: has it ever happened to you, to see someone fail or getting a very low score, just becasue she missed a definition?
Three months ago I witnessed an oral Mechanics test, a good one, overall, ending in failure because the student “confused moments with couples”: that didn’t mean, for example, inverting them within a Machine’s structure, resulting in a mess. The problem, here, was inverting the two definitions, even if, on the practical side, the same student proved to know their features and behavior.
Why is memorizing a definition evaluated as fundamental with respect to applying it? How am I supposed to fail even if I’m proving that I’m aware of both practical and theoretical aspects, even though I wasn’t able to pronounce the correct sequence of words?
Of course, it’s fundamental to be able both to define a feature and to utilize it, but, if there’s something that the failing student learned from the story I just told you, is that definitions is what we’re really tested on. Practice is still important, but if you have to allocate your energies, you’ll allocate their majority on memorizing sentences
So, what I’d do, in some cases, was just turning my inborn curiosity off, and steadily learning the Stokes theorem proof without a real understanding of the “real” implications, because I knew that they were seldom asked in tests, and my effort would have been wasted.
What I wish I knew before
Dear reader, don’t get me wrong: this post is not about what’s wrong with teaching.
As a matter of fact, it’s mostly about what’s wrong about me!
With this post I would like to offer (in case either teachers or students are reading) some critical insights, given by a student which has struggled a bit with traditional teaching, but that (I hope) has learned how to fill this gap.
Here’s some quick tips that made my life as a student easier and much more interesting since the immediate moment I started applying them:
- Chat GPT everything: well, not everything, not calculations indeed, but when it comes to rephrasing hard concepts, this tool made my life much easier. You can’t get over a step in Gauss-Green theorem’s proof? Your friendly neighborhood Pre-trained Transformer will give you a different and usually simple way to assess the problem.
When I studied Gauss-Green theorem, GPT 3 had just been released, and it sucked, but it helped me finding my way through the awful teacher’s notes that I posted before. Nowadays llm will by far outsmart the old ones in these tasks.
Simply prompting “Why is my teacher writing that…”, will make you progress… at least, it made me do that. - There always is a B plan: you feel like the “main” study material is insufficient or it doesn’t get along well with your pace? In 20s you can find some guy’s tutorial, or another handbook, or other people’s notes. It’s not the 70s anymore. Your teacher wants you to apply certain properties in the exact same way he did, considering wrong the other ones? First of all, shame on him. Second, go back to step 1 ;).
- Find a way to the Real World: you find stuff boring just because they look useless? So I did, how wrong I was! Have you ever googled (or asked Chat GPT 👀) which are practical applications of a Bode diagram? You’ll be left speechless!
- Last, don’t panic and don’t get mad. I used to get mad at least once a day, loosing dozens of minutes thinking about how f*cking stupid my teachers were, as, in that moment, they were a true enemy (well, a nice slice of guilt is as mine as teacher’s, but that’s not the right approach).
The truth is that you have a goal and you must find your way to do it as best as you can. Everything that brings you further from that must be erased. No excuses allowed 🙂
At the end of the day, learning isn’t about blindly memorizing formulas or struggling through abstract concepts in isolation. It’s about making connections—between theory and practice, between knowledge and curiosity. If I could go back, I’d remind myself that there’s always another way to understand something, another resource to turn to, and another reason to keep going. So, whether you’re just starting out or feeling stuck, don’t lose sight of why you’re here. Find your own way to make sense of things, and most importantly, don’t let frustration kill your curiosity.
Keep learning, keep questioning, and remember—you’re not alone in this.